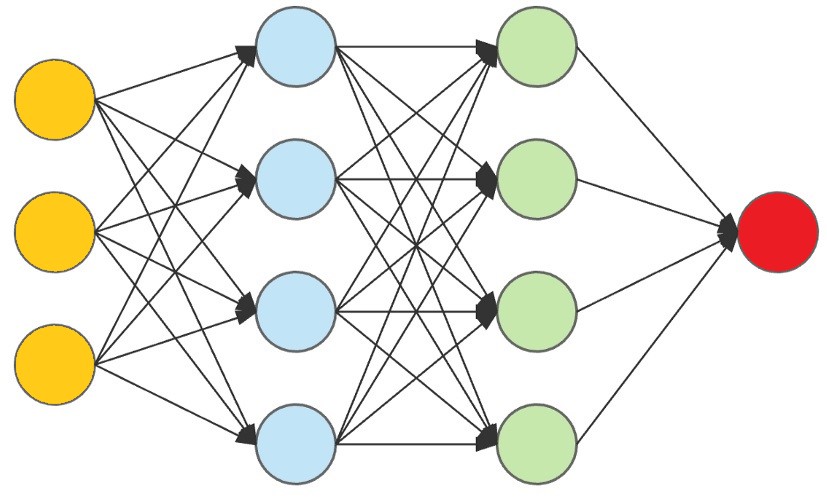
感知器
A 感知器 是一个人工神经元.
这是最简单的 神经网络.
神经网络 是机器学习.
弗兰克·罗森布拉特
弗兰克·罗森布拉特 (1928 – 1971) 是一位在人工智能领域著名的美国心理学家。
在 1957 他开始做一件大事。他“发明”了一种感知器 程序在康奈尔航空实验室的 IBM 704 计算机上运行。
科学家发现脑细胞(神经元)通过电信号接收来自我们感官的输入。
另一方面,神经元使用电信号来存储信息,并根据先前的输入做出决策。
弗兰克认为 感知器 可以模拟大脑原理,具有学习和决策的能力。
感知器
原本的 感知器 旨在采取一些二进制 输入,并产生一个二进制 输出(0 或 1)。
这个想法是使用不同的 重量 代表每一个的重要性输入,并且值的总和应该大于 临界点 在做出决定之前要考虑价值是的 或者不 (真或假)(0 或 1)。
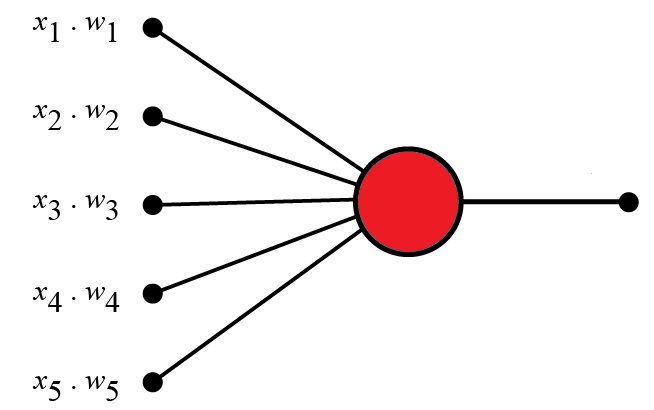
感知器示例
想象一个感知器(在你的大脑中)。
感知器试图决定你是否应该去听音乐会。
艺术家好吗?天气好吗?
这些事实应该具有什么样的分量?
| 标准 | 输入 | 重量 |
|---|---|---|
| 艺术家很好 | x1 = 0 或 1 | w1 = 0.7 |
| 天气很好 | x2 = 0 或 1 | w2 = 0.6 |
| 朋友会来 | x3 = 0 或 1 | w3 = 0.5 |
| 食物已送达 | x4 = 0 或 1 | w4 = 0.3 |
| 提供酒精饮料 | x5 = 0 或 1 | w5 = 0.4 |
感知器算法
Frank Rosenblatt 提出了这种算法:
- 设置阈值
- 将所有输入与其权重相乘
- 将所有结果相加
- 激活输出
1. 设定阈值:
- 阈值 = 1.5
2. 将所有输入与其权重相乘:
- x1 * w1 = 1 * 0.7 = 0.7
- x2 * w2 = 0 * 0.6 = 0
- x3 * w3 = 1 * 0.5 = 0.5
- x4 * w4 = 0 * 0.3 = 0
- x5 * w5 = 1 * 0.4 = 0.4
3. 将所有结果相加:
- 0.7 + 0 + 0.5 + 0 + 0.4 = 1.6(加权和)
4. 激活输出:
- 如果总和 > 1.5 (“是的,我会去听音乐会”),则返回 true
笔记
如果天气权重对于您来说是 0.6,那么对于其他人来说可能有所不同。权重越高意味着天气对他们越重要。
如果对你来说阈值是 1.5,对其他人来说可能就不一样了。阈值越低,意味着他们越想去听音乐会。
例子
常量阈值=1.5;
const 输入 = [1, 0, 1, 0, 1];
const 权重 = [0.7, 0.6, 0.5, 0.3, 0.4];
设总和=0;
对于(让 i = 0; i < 输入.长度; i++){
总和 += 输入[i] * 权重[i];
}
const 激活 = (总和 > 1.5);
感知器术语
- 感知器输入(节点)
- 节点值 (1, 0, 1, 0, 1)
- 节点权重(0.7、0.6、0.5、0.3、0.4)
- 激活函数(总和 > 阈值)
节点(感知器输入)
感知器输入称为 节点.
节点都具有 价值 和一个重量.
节点值(输入值)
每个输入节点都有一个二进制值 1 或者0.
这可以解释为 真的 或者错误的 / 是的 或者不.
在上面的例子中,节点值为: 1, 0, 1, 0, 1
节点权重
权重显示 力量 每个节点的。
在上面的例子中,节点权重为: 0.7, 0.6, 0.5, 0.3, 0.4
激活函数
激活函数将加权和映射为二进制值 1 或者0.
这可以解释为 真的 或者错误的 / 是的 或者不.
在上面的例子中,激活函数很简单: (总和 > 1.5)
笔记
显然,决定不是由 一个神经元 独自的。
许多其他神经元必须提供输入:
- 艺术家好吗
- 天气好吗
- ...
多层感知器 可用于非常复杂的决策。
神经网络
这 感知器 定义第一步神经网络: